區塊鏈共識算法的發展現狀與展望
發布時間:2019-07-12 11:14:18
共識算法是區塊鏈技術的核心要素,也是近年來分布式系統研究的熱點.本文系統性地梳理和討論了區塊鏈發展過程中的32種重要共識算法,介紹了傳統分布式一致性算法以及分布式共識領域的里程碑式的重要研究和結論,提出了區塊鏈共識算法的一種基礎模型和分類方法,并總結了現有共識算法的發展脈絡和若干性能指標,以期為未來共識算法的創新和區塊鏈技術的發展提供參考.
【摘要】 共識算法是區塊鏈技術的核心要素,也是近年來分布式系統研究的熱點.本文系統性地梳理和討論了區塊鏈發展過程中的32種重要共識算法,介紹了傳統分布式一致性算法以及分布式共識領域的里程碑式的重要研究和結論,提出了區塊鏈共識算法的一種基礎模型和分類方法,并總結了現有共識算法的發展脈絡和若干性能指標,以期為未來共識算法的創新和區塊鏈技術的發展提供參考.
【關鍵詞】 區塊鏈 共識算法 分布式系統 拜占庭容錯 P2P網絡
引用格式 袁勇, 倪曉春, 曾帥, 王飛躍. 區塊鏈共識算法的發展現狀與展望[J]. 自動化學報, 2018, 44(11): 2011-2022.
Blockchain Consensus Algorithms: The State of the Art and Future Trends
YUAN Yong, NI Xiao-Chun ZENG Shuai, WANG Fei-Yue
Abstract Consensus algorithm is a key component of the blockchain technology, and also a hot topic in distributed systems research. In this paper, we systematically review and discuss 32 mainstream consensus algorithms emerged in the development process of blockchain. We introduce the classic distributed consistency algorithms, as well as the milestone research efforts and the key conclusions of distributed consensus algorithms. We also propose a novel model and classification approach of blockchain consensus algorithms. In the end, we summarize the consensus algorithms and their performance measures using an evolutionary tree. This is our preliminary research effort towards the blockchain consensus algorithm, aiming at offering useful guidance and reference for future innovation of novel consensus algorithms and the development of blockchain technology.
Key words Blockchain consensus algorithms distributed systems Byzantine fault tolerance peer-to-peer network (P2P)
Citation Yuan Yong, Ni Xiao-Chun, Zeng Shuai, Wang Fei-Yue, Blockchain Consensus Algorithms: The State of the Art and Future Trends. Acta Automatica Sinica, 2018, 44(11): 2011-2022.
共識問題是社會科學和計算機科學等領域的經典問題, 已經有很長的研究歷史.目前有記載的文獻至少可以追溯到1959年, 蘭德公司和布朗大學的埃德蒙·艾森伯格(Edmund Eisenberg)和大衛·蓋爾(David Gale)發表的“Consensus of subjective probabilities: the parimutuel method”, 主要研究針對某個特定的概率空間, 一組個體各自有其主觀的概率分布時, 如何形成一個共識概率分布的問題[1].隨后, 共識問題逐漸引起了社會學、管理學、經濟學、特別是計算機科學等各學科領域的廣泛研究興趣.
計算機科學領域的早期共識研究一般聚焦于分布式一致性, 即如何保證分布式系統集群中所有節點的數據完全相同并且能夠對某個提案達成一致的問題, 是分布式計算的根本問題之一.雖然共識(Consensus)和一致性(Consistency)在很多文獻和應用場景中被認為是近似等價和可互換使用的, 但二者涵義存在著細微的差別:共識研究側重于分布式節點達成一致的過程及其算法, 而一致性研究則側重于節點共識過程最終達成的穩定狀態; 此外, 傳統分布式一致性研究大多不考慮拜占庭容錯問題, 即假設不存在惡意篡改和偽造數據的拜占庭節點, 因此在很長一段時間里, 傳統分布式一致性算法的應用場景大多是節點數量有限且相對可信的分布式數據庫環境.與之相比, 區塊鏈系統的共識算法則必須運行于更為復雜、開放和缺乏信任的互聯網環境下, 節點數量更多且可能存在惡意拜占庭節點.因此, 即使Viewstamped replication (VR)和Paxos等許多分布式一致性算法早在上世紀80年代就已經提出, 但是如何跨越拜占庭容錯這道鴻溝、設計簡便易行的分布式共識算法, 仍然是分布式計算領域的難題之一.
2008年10月31日, 一位化名為“中本聰”的研究者在密碼學郵件組中發表了比特幣的奠基性論文“Bitcoin: a peer-to-peer electronic cash system”[2], 基于區塊鏈(特別是公有鏈)的共識研究自此拉開序幕.從分布式計算和共識的角度來看, 比特幣的根本性貢獻在于首次實現和驗證了一類實用的、互聯網規模的拜占庭容錯算法, 從而打開了通往區塊鏈新時代的大門.
一般而言, 區塊鏈系統的節點具有分布式、自治性、開放可自由進出等特性, 因而大多采用對等式網絡(Peer-to-peer network, P2P網絡)來組織散布全球的參與數據驗證和記賬的節點. P2P網絡中的每個節點均地位對等且以扁平式拓撲結構相互連通和交互, 不存在任何中心化的特殊節點和層級結構, 每個節點均會承擔網絡路由、驗證區塊數據、傳播區塊數據、發現新節點等功能.區塊鏈系統采用特定的經濟激勵機制來保證分布式系統中所有節點均有動機參與數據區塊的生成和驗證過程, 按照節點實際完成的工作量分配共識過程所產生的數字加密貨幣, 并通過共識算法來選擇特定的節點將新區塊添加到區塊鏈.以比特幣為代表的一系列區塊鏈應用的蓬勃發展, 彰顯了區塊鏈技術的重要性與應用價值, 區塊鏈系統的共識也成為一個新的研究熱點[3-5].
迄今為止, 研究者已經在共識相關領域做了大量研究工作, 不同領域研究者的側重點也各不相同.計算機學科通常稱為共識算法或者共識協議, 管理和經濟學科則通常稱為共識機制.細究之下, 這些提法存在細微的差異:算法一般是一組順序敏感的指令集且有明確的輸入和輸出; 而協議和機制則大多是一組順序不敏感的規則集.就區塊鏈領域而言, 本文認為比特幣和以太坊等可認為是底層協議或機制, 其詳細規定了系統或平臺內部的節點交互規則、數據路由和轉發規則、區塊構造規則、交易驗證規則、賬本維護規則等集合; 而工作量證明(Proof-of-work, PoW)、權益證明(Proof-of-stake, PoS)等則是建立在特定協議或機制基礎上、可靈活切換的算法, 其規定了交易偵聽與打包、構造區塊、記賬人選舉、區塊傳播與驗證、主鏈選擇與更新等若干類順序敏感的指令集合.因此, 本文后續敘述均采用共識算法的提法.
現有文獻研究的共識問題實際上可以分為算法共識和決策共識兩個分支, 前者致力于研究在特定的網絡模型和故障模型前提下, 如何在缺乏中央控制和協調的分布式網絡中確保一致性, 其實質是一種“機器共識”; 后者則更為廣泛地研究無中心的群體決策中, 如何就最優的決策達成一致的問題, 例如關于比特幣系統擴容[6]問題和分叉問題的社區討論與路線選擇, 其實質是“人的共識”.二者的區別在于:前者是機器間的確定性共識, 以工程復雜性為主; 而后者則是以“人在環路中(Human-in-the-loop)”的復雜系統為特點的不確定性共識, 以社會復雜性為主.區塊鏈共識算法研究應屬于算法共識分支的子集, 而決策共識則大多見于分布式人工智能、多智能體等研究領域.
拜占庭將軍問題是分布式共識的基礎, 也是上述兩個研究分支的根源.拜占庭將軍問題有兩個交互一致性條件, 即一致性和正確性.由于大多數情況下, 正確性涉及到人的主觀價值判斷, 很難施加到分布式節點上, 因此算法共識采用的是“降級的正確性(Degraded correctness)”, 即從“表達的內容是正確的”降級為“正確地表達”, 這就導致區塊鏈的拜占庭共識實際上是一種機器共識, 其本身等價于分布式一致性+正確表達(不篡改消息).與之相對的是, 決策共識可以認為是人的共識, 不僅要求一致性, 而且要求所有節點相信“表達的內容是正確的”, 因而決策共識不僅要求內容的客觀一致性, 而且還要求其在共識節點間的主觀正確性.由此可見, 算法共識處理的是客觀的二值共識, 即對(唯一正確的賬本)和錯(所有錯誤的賬本), 而決策共識處理的是主觀的多值共識, 即意見1 (及其所屬群體)、意見2 (及其所屬群體)、…、意見N (及其所屬群體), 各節點最終通過群體間的協調和協作過程收斂到唯一意見(共識), 而此過程可能失敗(不收斂).
本文致力于按時間順序梳理和討論區塊鏈發展過程中的共識算法, 以期為未來共識算法的創新和區塊鏈技術的發展提供參考.本文的后續章節安排如下:首先, 簡要介紹了分布式共識領域重要的里程碑式的研究和結論, 包括兩軍問題、拜占庭問題和FLP不可能定理, 并介紹了傳統的分布式一致性算法; 然后, 提出了區塊鏈共識算法的一種基礎模型和分類方法, 并對當前主流的區塊鏈共識算法進行了分析; 最后, 總結了區塊鏈共識算法的發展和研究趨勢.
1 傳統分布式一致性算法
1975年, 紐約州立大學石溪分校的阿克云盧(Akkoyunlu E. A.)、埃卡納德漢姆(Ekanadham K.)和胡貝爾(Huber R. V.)在論文“Some constraints and tradeoffs in the design of network communications”中首次提出了計算機領域的兩軍問題及其無解性證明[7], 著名的數據庫專家吉姆·格雷正式將該問題命名為“兩軍問題”[8].兩軍問題表明, 在不可靠的通信鏈路上試圖通過通信達成一致共識是不可能的, 這被認為是計算機通信研究中第一個被證明無解的問題.兩軍問題對計算機通信研究產生了重要的影響, 互聯網時代最重要的TCP/IP協議中的“三次握手”過程即是為解決兩軍問題不存在理論解而誕生的簡單易行、成本可控的“工程解”.
分布式計算領域的共識問題于1980年由馬歇爾·皮斯(Marshall Pease)、羅伯特·肖斯塔克(Robert Shostak)和萊斯利·蘭伯特(Leslie Lamport)提出[9], 該問題主要研究在一組可能存在故障節點、通過點對點消息通信的獨立處理器網絡中, 非故障節點如何能夠針對特定值達成一致共識. 1982年, 作者在另一篇文章中正式將該問題命名為“拜占庭將軍問題”[10], 提出了基于口頭消息和基于簽名消息的兩種算法來解決該問題.拜占庭假設是對現實世界的模型化, 強調的是由于硬件錯誤、網絡擁塞或斷開以及遭到惡意攻擊, 計算機和網絡可能出現的不可預料的行為.此后, 分布式共識算法可以分為兩類, 即拜占庭容錯和非拜占庭容錯類共識.早期共識算法一般為非拜占庭容錯算法, 例如廣泛應用于分布式數據庫的VR和Paxos, 目前主要應用于聯盟鏈和私有鏈; 2008年末, 比特幣等公有鏈誕生后, 拜占庭容錯類共識算法才逐漸獲得實際應用.需要說明的是, 拜占庭將軍問題是區塊鏈技術核心思想的根源, 直接影響著區塊鏈系統共識算法的設計和實現, 因而在區塊鏈技術體系中具有重要意義.
1985年, 邁克爾·費舍爾(Michael Fisher)、南希·林奇(Nancy Lynch)和邁克爾·帕特森(Michael Paterson)共同發表了論文“Impossibility of distributed consensus with one faulty process”[11].這篇文章證明:在含有多個確定性進程的異步系統中, 只要有一個進程可能發生故障, 那么就不存在協議能保證有限時間內使所有進程達成一致.按照作者姓氏的首字母, 該定理被命名為FLP不可能定理, 是分布式系統領域的經典結論之一, 并由此獲得了Dijkstra獎. FLP不可能定理同樣指出了存在故障進程的異步系統的共識問題不存在有限時間的理論解, 因而必須尋找其可行的“工程解”.為此, 研究者們只能通過調整問題模型來規避FLP不可能定理, 例如犧牲確定性、增加時間等; 加密貨幣則是通過設定網絡同步性(或弱同步性)和時間假設來規避FLP不可能性, 例如網絡節點可以快速同步, 且礦工在最優鏈上投入有限時間和資源等.
早期的共識算法一般也稱為分布式一致性算法.與目前主流的區塊鏈共識算法相比, 分布式一致性算法主要面向分布式數據庫操作、且大多不考慮拜占庭容錯問題, 即假設系統節點只發生宕機和網絡故障等非人為問題, 而不考慮惡意節點篡改數據等問題. 1988年, 麻省理工學院的布萊恩·奧奇(Brian M. Oki)和芭芭拉·里斯科夫(Barbara H. Liskov, 著名計算機專家、2008年圖靈獎得主)提出了VR一致性算法, 采用主機-備份(Primary-backup)模式, 規定所有數據操作都必須通過主機進行, 然后復制到各備份機器以保證一致性[12]. 1989年, 萊斯利·蘭伯特(Leslie Lamport)在工作論文“The part-time parliament”中提出Paxos算法, 由于文章采用了講故事的敘事風格且內容過于艱深晦澀, 直到1998年才通過評審、發表在ACM transactions on computer systems期刊上[13]. Paxos是基于消息傳遞的一致性算法, 主要解決分布式系統如何就某個特定值達成一致的問題.隨著分布式共識研究的深入, Paxos算法獲得了學術界和工業界的廣泛認可, 并衍生出Abstract paxos、Classic paxos、Byzantine paxos和Disk paxos等變種算法, 成為解決異步系統共識問題最重要的算法家族[14].實際上, Liskove等提出的VR算法本質上也是一類Paxos算法.需要說明的是, VR和Paxos算法均假設系統中不存在拜占庭故障節點, 因而是非拜占庭容錯的共識算法.除以上共識算法外, 獲得較多研究關注的早期共識算法還有兩階段提交(Two-phase commit)算法、三階段提交(Three-phase commit)算法、Zab、Zyzzyva、Kafka等, 本文限于篇幅不加詳述.
2 主流區塊鏈共識算法
1993年, 美國計算機科學家、哈佛大學教授辛西婭·德沃克(Cynthia Dwork)首次提出了工作量證明思想[15], 用來解決垃圾郵件問題.該機制要求郵件發送者必須算出某個數學難題的答案來證明其確實執行了一定程度的計算工作, 從而提高垃圾郵件發送者的成本. 1997年, 英國密碼學家亞當·伯克(Adam Back)也獨立地提出、并于2002年正式發表了用于哈希現金(Hash cash)的工作量證明機制[16].哈希現金也是致力于解決垃圾郵件問題, 其數學難題是尋找包含郵件接受者地址和當前日期在內的特定數據的SHA-1哈希值, 使其至少包含20個前導零. 1999年, 馬庫斯·雅各布松(Markus Jakobsson)正式提出了“工作量證明”概念[17].這些工作為后來中本聰設計比特幣的共識機制奠定了基礎.
1999年, Barbara Liskov等提出了實用拜占庭容錯算法(Practical Byzantine fault tolerance, PBFT)[18], 解決了原始拜占庭容錯算法效率不高的問題, 將算法復雜度由指數級降低到多項式級, 使得拜占庭容錯算法在實際系統應用中變得可行. PBFT實際上是Paxos算法的變種, 通過改進Paxos算法使其可以處理拜占庭錯誤, 因而也稱為Byzantine paxos算法, 可以在保證活性(Liveness)和安全性(Safety)的前提下提供(n?1)/3 的容錯性, 其中n 為節點總數.
2000年, 加利福尼亞大學的埃里克·布魯爾(Eric Brewer)教授在ACM Symposium on Principles of Distributed Computing研討會的特邀報告中提出了一個猜想:分布式系統無法同時滿足一致性(Consistency)、可用性(Availability)和分區容錯性(Partition tolerance), 最多只能同時滿足其中兩個.其中, 一致性是指分布式系統中的所有數據備份在同一時刻保持同樣的值; 可用性是指集群中部分節點出現故障時, 集群整體是否還能處理客戶端的更新請求; 分區容忍性則是指是否允許數據分區, 不同分區的集群節點之間無法互相通信. 2002年, 塞斯·吉爾伯特(Seth Gilbert)和南希·林奇(Nancy Lynch)在異步網絡模型中證明了這個猜想, 使其成為CAP (Consistency, availability, partition tolerance)定理或布魯爾定理[19].該定理使得分布式網絡研究者不再追求同時滿足三個特性的完美設計, 而是不得不在其中做出取舍, 這也為后來的區塊鏈體系結構設計帶來了影響和限制.
2008年10月, 中本聰發表的比特幣創世論文催生了基于區塊鏈的共識算法研究.前文所提到的傳統分布式一致性算法大多應用于相對可信的聯盟鏈和私有鏈, 而面向比特幣、以太坊等公有鏈環境則誕生了PoW、PoS等一系列新的拜占庭容錯類共識算法.
比特幣采用了PoW共識算法來保證比特幣網絡分布式記賬的一致性, 這也是最早和迄今為止最安全可靠的公有鏈共識算法. PoW的核心思想是通過分布式節點的算力競爭來保證數據的一致性和共識的安全性.比特幣系統的各節點(即礦工)基于各自的計算機算力相互競爭來共同解決一個求解復雜但是驗證容易的SHA256數學難題(即挖礦), 最快解決該難題的節點將獲得下一區塊的記賬權和系統自動生成的比特幣獎勵. PoW共識在比特幣中的應用具有重要意義, 其近乎完美地整合了比特幣系統的貨幣發行、流通和市場交換等功能, 并保障了系統的安全性和去中心性.然而, PoW共識同時存在著顯著的缺陷, 其強大算力造成的資源浪費(主要是電力消耗)歷來為人們所詬病, 而且長達10分鐘的交易確認時間使其相對不適合小額交易的商業應用[3].
2011年7月, 一位名為Quantum Mechanic的數字貨幣愛好者在比特幣論壇(www.bitcointalk.org)首次提出了權益證明PoS共識算法[20].隨后, Sunny King在2012年8月發布的點點幣(Peercoin, PPC)中首次實現. PoS由系統中具有最高權益而非最高算力的節點獲得記賬權, 其中權益體現為節點對特定數量貨幣的所有權, 稱為幣齡或幣天數(Coin days). PPC將PoW和PoS兩種共識算法結合起來, 初期采用PoW挖礦方式以使得Token相對公平地分配給礦工, 后期隨著挖礦難度增加, 系統將主要由PoS共識算法維護. PoS一定程度上解決了PoW算力浪費的問題, 并能夠縮短達成共識的時間, 因而比特幣之后的許多競爭幣都采用PoS共識算法.
2013年2月, 以太坊創始人Vitalik Buterin在比特幣雜志網站詳細地介紹了Ripple (瑞波幣)及其共識過程的思路. Ripple項目實際上早于比特幣, 2004年就由瑞安·福格爾(Ryan Fugger)實現, 其初衷是創造一種能夠有效支持個人和社區發行自己貨幣的去中心化貨幣系統; 2014年, 大衛·施瓦爾茨(David Schwartz)等提出了瑞波協議共識算法(Ripple Protocol Consensus Algorithm, RPCA)[21], 該共識算法解決了異步網絡節點通訊時的高延遲問題, 通過使用集體信任的子網絡(Collectively-trusted subnetworks), 在只需最小化信任和最小連通性的網絡環境中實現了低延遲、高魯棒性的拜占庭容錯共識算法.目前, Ripple已經發展為基于區塊鏈技術的全球金融結算網絡.
2013年8月, 比特股(Bitshares)項目提出了一種新的共識算法, 即授權股份證明算法(Delegated proof-of-stake, DPoS)[22]. DPoS共識的基本思路類似于“董事會決策”, 即系統中每個節點可以將其持有的股份權益作為選票授予一個代表, 獲得票數最多且愿意成為代表的前N 個節點將進入“董事會”, 按照既定的時間表輪流對交易進行打包結算、并且簽署(即生產)新區塊[3].如果說PoW和PoS共識分別是“算力為王”和“權益為王”的記賬方式的話, DPoS則可以認為是“民主集中式”的記賬方式, 其不僅能夠很好地解決PoW浪費能源和聯合挖礦對系統的去中心化構成威脅的問題, 也能夠彌補PoS中擁有記賬權益的參與者未必希望參與記賬的缺點, 其設計者認為DPoS是當時最快速、最高效、最去中心化和最靈活的共識算法.
2013年, 斯坦福大學的迭戈·翁伽羅(Diego Ongaro)和約翰·奧斯特豪特(John Ousterhout)提出了Raft共識算法.正如其論文標題“In search of an understandable consensus algorithm”[23]所述, Raft的初衷是為設計一種比Paxos更易于理解和實現的共識算法.要知道, 由于Paxos論文極少有人理解, Lamport于2001年曾專門寫過一篇文章“Paxos made simple”[24], 試圖簡化描述Paxos算法但效果不好, 這也直接導致了Raft的提出.目前, Raft已經在多個主流的開源語言中得以實現.
3 共識算法的模型與分類
隨著比特幣的普及和區塊鏈技術的發展, 越來越多的新共識算法被提出.為使讀者更為深刻地理解不同的共識算法, 本節給出區塊鏈共識過程的一個主流模型.需要說明的是, 該模型并非通用模型, 可能無法涵蓋所有種類的共識過程, 但是可以體現大多數主流共識算法的核心思想.
區塊鏈系統建立在P2P網絡之上, 其全體節點的集合可記為P, 一般分為生產數據或者交易的普通節點, 以及負責對普通節點生成的數據或者交易進行驗證、打包、更新上鏈等挖礦操作的“礦工”節點集合(記為M), 兩類節點可能會有交集; 礦工節點通常情況下會全體參與共識競爭過程, 在特定算法中也會選舉特定的代表節點、代替它們參加共識過程并競爭記賬權, 這些代表節點的集合記為D; 通過共識過程選定的記賬節點記為A. 共識過程按照輪次重復執行, 每一輪共識過程一般重新選擇該輪的記賬節點.共識過程的核心是“選主”和“記賬”兩部分, 在具體操作過程中每一輪可以分為選主(Leader election)、造塊(Block generation)、驗證(Data validation)和上鏈(Chain updation, 即記賬) 4個階段.如圖 1所示, 共識過程的輸入是數據節點生成和驗證后的交易或數據, 輸出則是封裝好的數據區塊以及更新后的區塊鏈. 4個階段循環往復執行, 每執行一輪將會生成一個新區塊.
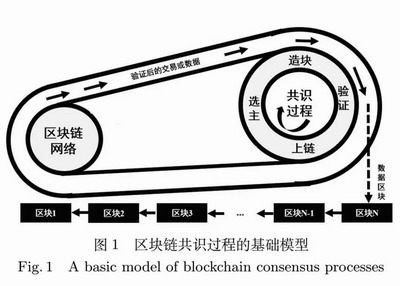
第1階段: 選主.選主是共識過程的核心, 即從全體礦工節點集M 中選出記賬節點A 的過程:我們可以使用公式f(M)→ A 來表示選主過程, 其中函數f 代表共識算法的具體實現方式.一般來說, |A|=1, 即最終選擇唯一的礦工節點來記賬.
第2階段: 造塊.第一階段選出的記賬節點根據特定的策略將當前時間段內全體節點P生成的交易或者數據打包到一個區塊中, 并將生成的新區塊廣播給全體礦工節點M 或其代表節點D. 這些交易或者數據通常根據區塊容量、交易費用、交易等待時間等多種因素綜合排序后, 依序打包進新區塊.造塊策略是區塊鏈系統性能的關鍵因素, 也是貪婪交易打包、自私挖礦等礦工策略性行為的集中體現.
第3階段: 驗證.礦工節點M 或者代表節點D 收到廣播的新區塊后, 將各自驗證區塊內封裝的交易或者數據的正確性和合理性.如果新區塊獲得大多數驗證/代表節點的認可, 則該區塊將作為下一區塊更新到區塊鏈.
第4階段: 上鏈.記賬節點將新區塊添加到主鏈, 形成一條從創世區塊到最新區塊的完整的、更長的鏈條.如果主鏈存在多個分叉鏈, 則需根據共識算法規定的主鏈判別標準, 來選擇其中一條恰當的分支作為主鏈.
區塊鏈共識算法可以根據其容錯類型、部署方式和一致性程度等多個維度加以分類.例如, 根據容錯類型, 可以將區塊鏈共識算法分為拜占庭容錯和非拜占庭容錯兩類; 根據部署方式, 可以將區塊鏈共識算法分為公有鏈共識、聯盟鏈共識和私有鏈共識三類; 根據一致性程度, 還可以將區塊鏈共識算法分為強一致性共識和弱(最終)一致性共識等.本文提出一種按照共識過程的選主策略的新分類方法, 其優點在于便于刻畫共識算法的核心機理.具體來說, 可根據選主策略(即函數f 的具體實現方式)將區塊鏈共識算法分為選舉類、證明類、隨機類、聯盟類和混合類共5種類型:
選舉類共識:即礦工節點在每一輪共識過程中通過“投票選舉”的方式選出當前輪次的記賬節點, 首先獲得半數以上選票的礦工節點將會獲得記賬權; 多見于傳統分布式一致性算法, 例如Paxos和Raft等.
證明類共識:也可稱為“Proof of X”類共識, 即礦工節點在每一輪共識過程中必須證明自己具有某種特定的能力, 證明方式通常是競爭性地完成某項難以解決但易于驗證的任務, 在競爭中勝出的礦工節點將獲得記賬權; 例如PoW和PoS等共識算法是基于礦工的算力或者權益來完成隨機數搜索任務, 以此競爭記賬權.
隨機類共識:即礦工節點根據某種隨機方式直接確定每一輪的記賬節點, 例如下文將要提到的Algorand和PoET共識算法等.
聯盟類共識:即礦工節點基于某種特定方式首先選舉出一組代表節點, 而后由代表節點以輪流或者選舉的方式依次取得記賬權.這是一種以“代議制”為特點的共識算法, 例如DPoS等.
混合類共識:即礦工節點采取多種共識算法的混合體來選擇記賬節點, 例如PoW + PoS混合共識、DPoS+BFT共識等.
4 區塊鏈共識算法的新進展
自2014年起, 隨著比特幣和區塊鏈技術快速進入公眾視野, 許多學者開始關注并研究區塊鏈技術, 共識算法也因此進入快速發展、百花齊放的時期.許多新共識算法在這段時間被提出.它們或者是原有算法的簡單變種, 或者是為改進某一方面性能而做出的微創新, 或者是為適應新場景和新需求而做出重大改進的新算法.需要說明的是, 這些共識算法由于提出時間晚, 目前大多尚未獲得令人信服的實踐驗證, 有些甚至只是科研設想; 但這些算法均具有明顯的創新之處, 具有一定的大規模應用的前景, 因此我們寫出來以饗讀者, 并期待能夠啟發后續的創新研究.
4.1 主線一: PoW與PoS算法的有機結合
研究者基于PoW和PoS算法的有機結合, 相繼提出了權益-速度證明(Proof of stake velocity, PoSV)[25]、燃燒證明(Proof of burn, PoB)[26]、行動證明(Proof of activity, PoA)[27]和二跳(2-hop)[28]共識算法, 致力于取長補短、解決PoW與PoS存在的能源消耗與安全風險問題. 2014年4月, 拉里·雷恩(Larry Ren)在蝸牛幣Reddcoin白皮書中提出了PoSV共識算法, 針對PoS中幣齡是時間的線性函數這一問題進行改進, 致力于消除持幣人的屯幣現象. PoSV算法前期使用PoW實現代幣分配, 后期使用PoSV維護網絡長期安全. PoSV將PoS中幣齡和時間的線性函數修改為指數式衰減函數, 即幣齡的增長率隨時間減少最后趨于零.因此新幣的幣齡比老幣增長地更快, 直到達到上限閾值, 這在一定程度上緩和了持幣者的屯幣現象. 2014年5月發行的Slimcoin借鑒了比特幣和點點幣的設計, 基于PoW和PoS首創提出了PoB共識算法.其中, PoW共識被用來產生初始的代幣供應, 隨著時間增長, 區塊鏈網絡累積了足夠的代幣時, 系統將依賴PoB和PoS共識來共同維護. PoB共識的特色是礦工通過將其持有的Slimcoin發送至特定的無法找回的地址(燃燒)來競爭新區塊的記賬權, 燃燒的幣越多則挖到新區塊的概率越高. 2014年12月提出的PoA共識也是基于PoW和PoS, 其中采用PoW挖出的部分代幣以抽獎的方式分發給所有活躍節點, 而節點擁有的權益與抽獎券的數量即抽中概率成正比.二跳共識于2017年4月提出, 其設計初衷是為解決PoW潛在的51%算力攻擊問題, 解決思路是在PoW算力的基礎上引入PoS權益, 使得區塊鏈安全建立在誠實節點占有大多數聯合資源(算力+權益)的基礎上.換句話說, 拜占庭節點必須同時控制51%以上的算力和51%以上的權益, 才能成功實施51%攻擊, 這無疑極大地提高了區塊鏈的安全性.
4.2 主線二: 原生PoS算法的改進
原生PoS共識算法的改進目標主要是解決其固有的“無利害關系(Nothing at stake)”問題, 形成了Tendermint[29]以及由其衍生出的Casper[30]、Ouroboros[31]、Tezos[32]和Honeybadger[33]等新共識算法.原生PoS共識一般假設系統中的對等節點都是靜態和長期穩定的, 這在區塊鏈環境中并不現實. 2014年提出的Tendermint的重大突破是使用區塊、哈希鏈接、動態驗證器集合和循環的領導者選舉, 實現了第一個基于PBFT的PoS共識算法.為解決無利害關系問題, Tendermint節點需要繳納保證金, 如果作惡則保證金就會被沒收. Tendermint是一種拜占庭容錯的共識算法, 具有抵御雙花攻擊的魯棒性, 并且可以抵御網絡中至多三分之一的破壞者的攻擊.
2015年提出的Casper是以太坊計劃在其路線圖中稱為寧靜(Serenity)的第4階段采用的共識算法, 尚在設計、討論和完善階段.目前Casper總共有兩個版本, 即由Vlad Zamjir領導的Casper the friendly ghost (CTFG)[34]和由Vitalik Buterin帶領實現的Casper friendly finality gadget (CFFG)[35].前者是明確的PoS共識, 而后者則是PoW和PoS共識的有機結合.同時, PoS共識的兩個主要原理分別是基于鏈的PoS和基于拜占庭容錯的PoS. Tendermint是基于拜占庭容錯的PoS設計.相比之下, CTFG是基于鏈的PoS設計, 而CFFG則是兩者的結合.
2016年提出的HoneyBadger共識是首個實用的異步拜占庭容錯共識協議, 可以在沒有任何網絡時間假設的前提下保證區塊鏈系統的活性(Liveness).該共識基于一種可實現漸近有效性的原子廣播協議, 能夠在廣域網的上百個節點上處理每秒上萬筆交易. 2017年8月提出的Ouroboros共識是首個基于PoS并且具有嚴格安全性保障的區塊鏈協議, 其特色是提出了一種新的獎勵機制來驅動PoS共識過程, 使得誠實節點的行為構成一個近似納什均衡, 可以有效地抵御區塊截留和自私挖礦等由于礦工的策略性行為而導致的安全攻擊.
4.3 主線三: 原生PoW共識算法的改進
原生PoW共識算法的改進目標主要是實現比特幣擴容或者降低其能耗. 2016年3月, 康奈爾大學的Eyal等提出一種新的共識算法Bitcoin-NG[36], 將時間切分為不同的時間段.在每一個時間段上由一個領導者負責生成區塊、打包交易.該協議引入了兩種不同的區塊:用于選舉領導者的關鍵區塊和包含交易數據的微區塊.關鍵區塊采用比特幣PoW共識算法生成, 然后領導者被允許小于預設閾值的速率(例如10秒)來生成微區塊. Bitcoin-NG可在不改變區塊容量的基礎上通過選舉領導者生成更多的區塊, 從而可輔助解決比特幣的擴容問題.同年8月提出的ByzCoin[37]共識算法借鑒了Bitcoin-NG這種領導者選舉和交易驗證相互獨立的設計思想, 是一種新型的可擴展拜占庭容錯算法, 可使得區塊鏈系統在保持強一致性的同時, 達到超出Paypal吞吐量的高性能和低確認延遲. 2016年提出的Elastico[38]共識機制通過分片技術來增強區塊鏈的擴展性, 其思路是將挖礦網絡以可證明安全的方式隔離為多個分片(Shard), 這些分片并行地處理互不相交的交易集合. Elastico是第一個拜占庭容錯的安全分片協議. 2017年, OmniLedger[39]進一步借鑒ByzCoin和Elastico共識, 設計并提出名為ByzCoinX的拜占庭容錯協議. OmniLedger通過并行跨分片交易處理優化區塊鏈性能, 是第一種能夠提供水平擴展性而不必犧牲長期安全性和去中心性的分布式賬本架構.
為改進PoW共識算法的效率(能耗)和公平性, 研究者相繼提出了消逝時間證明(Proof of elapsed time, PoET)[40]和運氣證明(Proof of luck, PoL)[41]. PoET和PoL均是基于特定的可信執行環境(Trusted execution environments, TEE, 例如基于Intel SGX技術的CPU)的隨機共識算法. PoET是超級賬本HyperLedger的鋸齒湖Sawtooth項目采用的共識算法, 其基本思路是每個區塊鏈節點都根據預定義的概率分布生成一個隨機數, 來決定其距離下一次獲得記賬權的等待時間.每當一個新區塊提交到區塊鏈系統后, SGX即可幫助節點創建區塊、生成該等待時間的證明, 而這種證明易于被其他SGX節點驗證. PoET共識的意義在于使得區塊鏈系統不必消耗昂貴算力來挖礦、從而提高了效率, 同時也真正實現了“一CPU一票”的公平性.類似地, PoL共識也采用TEE平臺的隨機數生成器來選擇每一輪共識的領導者(記賬人), 從而可降低交易驗證延遲時間和交易確認時間、實現可忽略的能源消耗和真正公平的分布式挖礦.
2014年提出的空間證明(Proof of space, PoSp)[42]和2017年提出的有益工作證明(Proof of useful work, PoUW)[43]也是為解決PoW的能耗問題而提出的共識算法. PoSp共識要求礦工必須出具一定數量的磁盤空間(而非算力)來挖礦, 而PoUW則將PoW共識中毫無意義的SHA256哈希運算轉變為實際場景中既困難又有價值的運算, 例如計算正交向量問題、3SUM問題、最短路徑問題等.
4.4 主線四: 傳統分布式一致性算法的改進及其他
傳統分布式一致性算法大多是非拜占庭容錯的, 因而難以應用于區塊鏈場景(特別是公有鏈).為此, 克里斯托弗·科普蘭(Christopher Copeland)等結合Raft和PBFT算法的優勢, 于2014年提出拜占庭容錯的Tangaroa算法[44]. Tangaroa繼承了Raft簡潔和容易理解的優勢, 同時在拜占庭錯誤環境下也能夠維持安全性、容錯性和活性.受Tangaroa共識啟發, 2016年Github平臺的Juno項目提出一種拜占庭容錯的Raft算法, 此后該算法演變為一種稱為ScalableBFT[45]的專用拜占庭容錯協議, 能夠實現比Tangaroa和Juno更好的性能.
2015年, Stellar.org首席科學官David Mazieres教授提出了恒星共識協議(Stellar consensus protocol, SCP)[46]. SCP在聯邦拜占庭協議和Ripple協議的基礎上演化而來的, 是第一個可證明安全的共識機制, 具有分散控制、低延遲、靈活信任和漸近安全4個關鍵屬性.同年, 超級賬本的鋸齒湖項目將Ripple和SCP共識相結合, 提出了法定人數投票(Quorum voting)共識算法, 以應對那些需要即時交易最終性的應用場景. 2016年, 中國區塊鏈社區NEO (原名小蟻)提出一種改進的拜占庭容錯算法dBFT, 該算法在PBFT的基礎上借鑒了PoS設計思路, 首先按照節點的權益來選出記賬人, 然后記賬人之間通過拜占庭容錯算法來達成共識.該算法改進了PoW和PoS缺乏最終一致性的問題, 使得區塊鏈能夠適用于金融場景.
2016年, 圖靈獎得主、MIT教授Sivio Micali提出了一種稱為AlgoRand[47]的快速拜占庭容錯共識算法.該算法利用密碼抽簽技術選擇共識過程的驗證者和領導者, 并通過其設計的BA*拜占庭容錯協議對新區塊達成共識. AlgoRand只需極小計算量且極少分叉, 被認為是真正民主和高效的分布式賬本共識技術.
2017年, 康奈爾大學提出了一種稱為Sleepy Consensus (休眠共識)的新算法[48].這種共識針對的是互聯網環境下大規模的共識節點中可能多數都處于離線狀態, 僅有少數節點在線參與共識過程的實際情況.該研究證明, 傳統共識算法無法在這種環境下保證共識的安全性.而采用休眠共識算法, 只要在線誠實節點的數量超過故障節點的數量, 即可保證安全性和魯棒性.
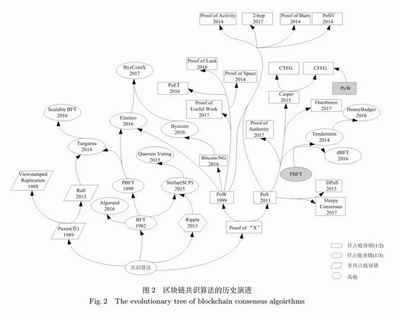
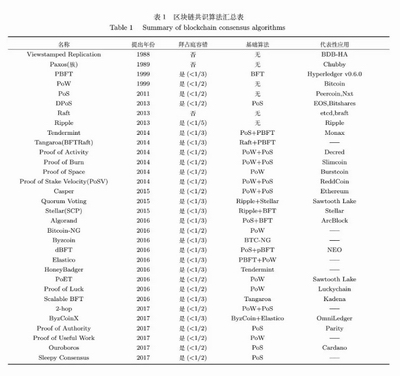
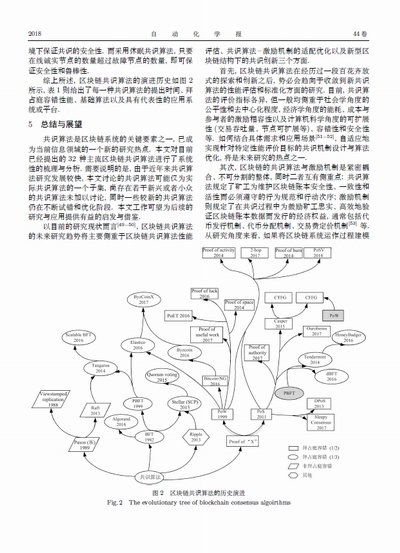
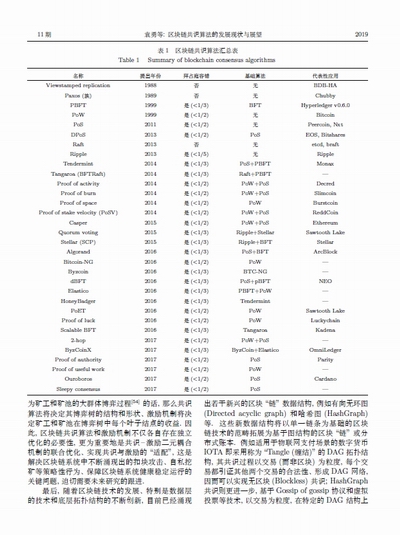
綜上所述, 區塊鏈共識算法的演進歷史如圖 2所示, 表 1則給出了每一種共識算法的提出時間、拜占庭容錯性能、基礎算法以及具有代表性的應用系統或平臺.
5 總結與展望
共識算法是區塊鏈系統的關鍵要素之一, 已成為當前信息領域的一個新的研究熱點.本文對目前已經提出的32種主流區塊鏈共識算法進行了系統性的梳理與分析.需要說明的是, 由于近年來共識算法研究發展較快, 本文討論的共識算法可能僅為實際共識算法的一個子集, 尚存在若干新興或者小眾的共識算法未加以討論, 同時一些較新的共識算法仍在不斷試錯和優化階段.本文工作可望為后續的研究與應用提供有益的啟發與借鑒.
以目前的研究現狀而言[49-50], 區塊鏈共識算法的未來研究趨勢將主要側重于區塊鏈共識算法性能評估、共識算法-激勵機制的適配優化以及新型區塊鏈結構下的共識創新三個方面.
首先, 區塊鏈共識算法在經歷過一段百花齊放式的探索和創新之后, 勢必會趨向于收斂到新共識算法的性能評估和標準化方面的研究.目前, 共識算法的評價指標各異, 但一般均側重于社會學角度的公平性和去中心化程度, 經濟學角度的能耗、成本與參與者的激勵相容性以及計算機科學角度的可擴展性(交易吞吐量、節點可擴展等)、容錯性和安全性等.如何結合具體需求和應用場景[51-52], 自適應地實現針對特定性能評價目標的共識機制設計與算法優化, 將是未來研究的熱點之一.
其次, 區塊鏈的共識算法與激勵機制是緊密耦合、不可分割的整體, 同時二者互有側重點:共識算法規定了礦工為維護區塊鏈賬本安全性、一致性和活性而必須遵守的行為規范和行動次序; 激勵機制則規定了在共識過程中為鼓勵礦工忠實、高效地驗證區塊鏈賬本數據而發行的經濟權益, 通常包括代幣發行機制、代幣分配機制、交易費定價機制[53]等.從研究角度來看, 如果將區塊鏈系統運作過程建模為礦工和礦池的大群體博弈過程[54]的話, 那么共識算法將決定其博弈樹的結構和形狀、激勵機制將決定礦工和礦池在博弈樹中每個葉子結點的收益.因此, 區塊鏈共識算法和激勵機制不僅各自存在獨立優化的必要性, 更為重要地是共識-激勵二元耦合機制的聯合優化、實現共識與激勵的“適配”, 這是解決區塊鏈系統中不斷涌現出的扣塊攻擊、自私挖礦等策略性行為、保障區塊鏈系統健康穩定運行的關鍵問題, 迫切需要未來研究的跟進.
最后, 隨著區塊鏈技術的發展、特別是數據層的技術和底層拓撲結構的不斷創新, 目前已經涌現出若干新興的區塊“鏈”數據結構, 例如有向無環圖(Directed acyclic graph)和哈希圖(HashGraph)等.這些新數據結構將以單一鏈條為基礎的區塊鏈技術的范疇拓展為基于圖結構的區塊“鏈”或分布式賬本.例如適用于物聯網支付場景的數字貨幣IOTA即采用稱為“Tangle (纏結)”的DAG拓撲結構, 其共識過程以交易(而非區塊)為粒度, 每個交易都引證其他兩個交易的合法性、形成DAG網絡, 因而可以實現無區塊(Blockless)共識; HashGraph共識則更進一步, 基于Gossip of gossip協議和虛擬投票等技術, 以交易為粒度, 在特定的DAG結構上實現公平和快速的拜占庭容錯共識.這些新型區塊拓撲結構及其共識算法是未來發展趨勢之一, 建立在這些新型數據結構之上的共識算法也值得深入研究.
參考文獻
|
1 |
Eisenberg E, Gale D. Consensus of subjective probabilities:the pari-mutuel method. The Annals of Mathematical Statistics, 1959, 30(1): 165-168. |
|
2 |
Nakamoto S. Bitcoin: a peer-to-peer electronic cash system[Online], available: http://bitcoins.info/bitcoin.pdf, April 10, 2018. |
|
3 |
Yuan Yong, Wang Fei-Yue. Blockchain:the state of the art and future trends. Acta Automatica Sinica, 2016, 42(4): 481-494. |
|
4 |
Yuan Yong, Zhou Tao, Zhou Ao-Ying, Duan Yong-Chao, Wang Fei-Yue. Blockchain technology:from data intelligence to knowledge automation. Acta Automatica Sinica, 2017, 43(9): 1485-1490. |
|
5 |
Yuan Yong, Wang Fei-Yue. Parallel blockchain:concept, methods and issues. Acta Automatica Sinica, 2017, 43(10): 1703-1712. |
|
6 |
Zeng Shuai, Yuan Yong, Ni Xiao-Chun, Wang Fei-Yue. Scaling blockchain towards bitcoin: key technologies, constraints and related issues. Acta Automatica Sinica. (曾帥, 袁勇, 倪曉春, 王飛躍.面向比特幣的區塊鏈擴容: 關鍵技術, 制約因素與衍生問題.自動化學報) |
|
7 |
Akkoyunlu E A, Ekanadham K, Huber R V. Some constraints and tradeoffs in the design of network communications. In: Proceedings of the 5th ACM Symposium on Operating Systems Principles. Austin, Texas, USA: ACM, 1975. 67-74 http://www.mendeley.com/research/some-constraints-tradeoffs-design-network-communications/ |
|
8 |
Gray J N. Notes on data base operating systems. Operating Systems: An Advanced Course. Berlin: Springer-Verlag, 1978. 393-481. |
|
9 |
Pease M, Shostak R, Lamport L. Reaching agreement in the presence of faults. Journal of the ACM, 1980, 27(2): 228-234. |
|
10 |
Lamport L, Shostak R, Pease M. The Byzantine generals problem. ACM Transactions on Programming Languages and Systems, 1982, 4(3): 382-401. |
|
11 |
Fischer M J, Lynch N A, Paterson M S. Impossibility of distributed consensus with one faulty process. Journal of the ACM, 1985, 32(2): 374-382. |
|
12 |
Oki B M, Liskov B H. Viewstamped replication: a new primary copy method to support highly-available distributed systems. In: Proceedings of the 7th Annual ACM Symposium on Principles of Distributed Computing. Toronto, Ontario, Canada: ACM, 1988. 8-17 http://www.mendeley.com/catalog/viewstamped-replication-new-primary-copy-method-support-highlyavailable-distributed-systems/ |
|
13 |
Lamport L. The part-time parliament. ACM Transactions on Computer Systems, 1998, 16(2): 133-169. |
|
14 |
Wattenhofer R. The Science of the Blockchain. USA: CreateSpace Independent Publishing Platform, 2016. |
|
15 |
Dwork C, Naor M. Pricing via processing or combatting junk mail. In: Proceedings of the 12th Annual International Cryptology Conference on Advances in Cryptology. Santa Barbara, California, USA: Springer-Verlag, 1992. 139-147 http://www.springerlink.com/content/l90we8aq0nre2a4n |
|
16 |
Back A. Hashcash-a denial of service counter-measure[Online], available: http://www.hashcash.org/papers/hashcash.pdf, April 10, 2018. |
|
17 |
Jakobsson M, Juels A. Proofs of work and bread pudding protocols (extended abstract). Secure Information Networks. Boston, MA, Germany: Springer, 1999. 258-272. |
|
18 |
Castro M, Liskov B. Practical Byzantine fault tolerance. In: Proceedings of the 3rd Symposium on Operating Systems Design and Implementation. New Orleans, USA: USENIX Association, 1999. 173-186 http://dl.acm.org/citation.cfm?id=296824 |
|
19 |
Gilbert S, Lynch N. Brewer's conjecture and the feasibility of consistent, available, partition-tolerant web services. ACM SIGACT News, 2002, 33(2): 51-59. DOI:10.1145/564585 |
|
20 |
Proof of stake[Online], available: https://en.bitcoin.it/wiki/Proof_of_Stake, April 11, 2018. |
|
21 |
Schwartz D, Youngs N, Britto A. The Ripple protocol consensus algorithm[Online], available: https://ripple.com/files/ripple_consensus_whitepaper.pdf, April 10, 2018. |
|
22 |
BitShares. Delegated proof of stake[Online], available: http://docs.bitshares.org/bitshares/dpos.html, April 10, 2018. |
|
23 |
Ongaro D, Ousterhout J. In search of an understandable consensus algorithm. In: Proceedings of the USENIX Annual Technical Conference. Philadelphia, PA, USA: USENIX ATC, 2014. 305-319 |
|
24 |
Lamport L. Paxos made simple. ACM SIGACT News, 2001, 32(4): 51-58. |
|
25 |
Ren L. Proof of stake velocity: building the social currency of the digital age[Online], available: https://assets.coss.io/documents/white-papers/reddcoin.pdf, April 10, 2018. |
|
26 |
Proof of burn[Online], available: https://en.bitcoin.it/wiki/Proof of burn, April 10, 2018. |
|
27 |
Bentov I, Lee C, Mizrahi A, Rosenfeld M. Proof of activity: extending Bitcoin's proof of work via proof of stake[Online], available: http://eprint.iacr.org/2014/452, April 10, 2018. |
|
28 |
Duong T, Fan L, Zhou H S. 2-hop blockchain: combining proof-of-work and proof-of-stake securely[Online], available: https://eprint.iacr.org/2016/716, April 10, 2018. |
|
29 |
Kwon J. Tendermint: consensus without mining[Online], available: https://tendermint.com/static/docs/ten-dermint.pdf, April 10, 2018. |
|
30 |
Ethereum's Casper protocol explained in simple terms[Online], available: https://www.finder.com/ethereum-casper, April 10, 2018. |
|
31 |
David B, Ga?i P, Kiayias A, Russell A. Ouroboros Praos: an adaptively-secure, semi-synchronous proof-of-stake protocol[Online], available: http://eprint.iacr.org/2017/573, April 10, 2018. |
|
32 |
Goodman L M. Tezos-a self-amending crypto-ledger position paper[Online], available: https://www.tezos.com/static/papers/position_paper.pdf, April 10, 2018. |
|
33 |
Miller A, Xia Y, Croman K, Shi E, Song D. The honey badger of BFT protocols. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. Vienna, Austria: ACM, 2016. 31-42 |
|
34 |
Zamfir V. Introducing Casper “the Friendly Ghost”[Online], available: https://blog.ethereum.org/2015/08/01/introducing-casper-friendly-ghost/, April 10, 2018. |
|
35 |
Buterin V, Griffith V. Casper the friendly finality gadget[Online], available: https://arxiv.org/pdf/1710.09437.pdf, April 10, 2018. |
|
36 |
Eyal I, Gencer A E, Sirer E G, van Renesse R. Bitcoin-NG: a scalable blockchain protocol. In: Proceedings of the 13th USENIX Conference on Networked Systems Design and Implementation. Santa Clara, USA: USENIX Association, 2016. 45-59 http://dl.acm.org/citation.cfm?id=2930615 |
|
37 |
Kogias E K, Jovanovic P, Gailly N, Khoffi I, Gasser L, Ford B. Enhancing bitcoin security and performance with strong consistency via collective signing. In: Proceedings of the 25th USENIX Security Symposium. Austin, TX, USA: USENIX Association, 2016. 279-296 http://memento.epfl.ch/event/enhancing-bitcoin-security-and-performance-with-st/ |
|
38 |
Luu L, Narayanan V, Zheng C D, Baweja K, Gilbert S, Saxena P. A secure sharding protocol for open blockchains. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. Vienna, Austria: ACM, 2016. 17-30 http://www.deepdyve.com/lp/association-for-computing-machinery/a-secure-sharding-protocol-for-open-blockchains-GYAJ0F0KdC |
|
39 |
Kokoris-Kogias E, Jovanovic P, Gasser L, Gailly N, Syta E, Ford B. OmniLedger: A secure, scale-out, decentralized ledger via sharding[Online], available: http://eprint.iacr.org/2017/406, April 10, 2018. |
|
40 |
Buntinx J P. What is proof of elapsed time?[Online], available: https://themerkle.com/what-is-proof-of-elapsed-time/, April 10, 2018. |
|
41 |
Milutinovic M, He W, Wu H, Kanwal M. Proof of luck: an efficient blockchain consensus protocol[Online], available: https://eprint.iacr.org/2017/249.pdf, April 10, 2018. |
|
42 |
Ateniese G, Bonacina I, Faonio A, Galesi A. Proofs of space: when space is of the essence. In: Proceedings of the 9th International Conference on Security and Cryptography for Networks. Amalfi, Italy: Springer, 2014. 538-557 https://link.springer.com/chapter/10.1007%2F978-3-319-10879-7_31 |
|
43 |
Ball M, Rosen A, Sabin M, Vasudevan P V. Proofs of useful work[Online], available: https://allquantor.at/blockchain-bib/pdf/ball2017proofs.pdf, April 10, 2018. |
|
44 |
Copeland C, Zhong H X. Tangaroa: a byzantine fault tolerant raft[Online], available: http://www.scs.stanford.edu/14au-cs244b/labs/projects/copeland_zhong.pdf, April 10, 2018. |
|
45 |
Martino W. Kadena: the first scalable, high performance private blockchain[Online], available: http://kadena.io/docs/Kadena-ConsensusWhitePaper-Aug2016.pdf, April 10, 2018. |
|
46 |
Maziéres D. The stellar consensus protocol: a federated model for internet-level consensus[Online], available: https://www.stellar.org/papers/stellar-consensus-protocol.pdf, April 10, 2018. |
|
47 |
Gilad Y, Hemo R, Micali S, Vlachos G, Zeldovich N. Algorand: scaling byzantine agreements for cryptocurrencies[Online], available: http://eprint.iacr.org/2017/454, April 10, 2018. |
|
48 |
Pass R, Shi E. The sleepy model of consensus[Online], available: https://eprint.iacr.org/2016/918.pdf, August 16, 2018. |
|
49 |
Yuan Y, Wang F Y. Blockchain and cryptocurrencies:model, techniques, and applications. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2018, 48(9): 1421-1428. |
|
50 |
Zeng S, Ni X C, Yuan Y, Wang F Y. A bibliometric analysis of blockchain research. In: Proceedings of the 29th IEEE Intelligent Vehicles Symposium (Ⅳ'18). Changshu, China: IEEE, 2018. 102-107 |
|
51 |
Ni X C, Zeng S, Han X, Yuan Y, Wang F Y. Organizational management using software-defined robots based on smart contracts. In: Proceedings of the 29th IEEE Intelligent Vehicles Symposium (Ⅳ'18). Changshu, China: IEEE, 2018. 274-279 |
|
52 |
Wang S, Yuan Y, Wang X, Li J J, Qin R, Wang F Y. An overview of smart contract: architecture, applications, and future trends. In: Proceedings of the 29th IEEE Intelligent Vehicles Symposium (Ⅳ'18). Changshu, China: IEEE, 2018. 108-113 |
|
53 |
Li J J, Yuan Y, Wang S, Wang F Y. Transaction queue game in bitcoin blockchain. In: Proceedings of the 29th IEEE Intelligent Vehicles Symposium (Ⅳ'18). Changshu, China: IEEE, 2018. 114-119 |
|
54 |
Qin R, Yuan Y, Wang S, Wang F Y. Economic issues in bitcoin minning and blockchain research. In: Proceedings of the 29th IEEE Intelligent Vehicles Symposium (Ⅳ'18). Changshu, China: IEEE, 2018. 268-273 |
后記:此文于2018年
/Uploads/image/file/20190712/20190712110112_58958.pdf










來源:王飛躍科學網博客